
Onde t designa o tempo, em segundos, e h a altura, em metros.
1.1 - Calcule a taxa média de variação nos dois primeiros segundos após o lançamento.
1.2 - Calcule a taxa média de variação no intervalo [t, t + h], com h a tender para zero.
1.3 - Calcule a velocidade da maça no instante t = 2.
1.4 - Escreva uma equação da recta tangente ao gráfico de h no ponto de abcissa 1.
Resolução:
1.1 - Atendendo à expressão que permite calcular a taxa média de variação num intervalo [a,b], temos:
1.2 -

Como h tende para zero, temos:
1.3 - Pela definição de derivada, podemos concluir que h´ (t) = 8 – 2t.
Como a velocidade no instante t=2 corresponde á derivada de h no ponto de abcissa 2, temos então que:

A velocidade da maça no instante t=2 é de 4 m/
1.4 - Para escrever uma equação da recta tangente é necessário conhecer as coordenadas do ponto de tangencia, assim como o declive da recta.
O ponto de tangente tem abcissa igual a 1, logo, a coordenada é h (1)
Assim, o ponto de tangente tem de coordenadas (1,9)
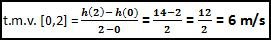


Um balão está a 60 m acima do solo e se eleva verticalmente à razão de 5 m/s. Um automóvel
ResponderEliminarpassa por baixo do balão viajando à 12 m/s. Com que velocidade varia, um segundo depois, a
distância entre o balão e o automóvel?
Voce saberia responder essa questão?
Muitissimo obrgdo, entendi
ResponderEliminarMuitissimo obrgdo, entendi
ResponderEliminarCalcule a taxa de variação instantânea.
ResponderEliminarResposta: