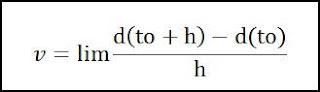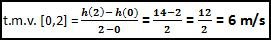História da Taxa de Variação

Se quiser saber a história da taxa de Variação clique aqui !!

http://matematica-taxavariacao.hi5.com/

Taxa de Variação - Definições

Taxa média de variação – Para medir a maior ou menor rapidez de variação de uma função f, num intervalo [a, b], recorre-se ao seguinte quociente:

A que se chama taxa média de variação (tmv) de f, no intervalo [a, b].

Velocidade média – Quando uma função é em particular, uma lei espacial, ou seja, uma relação espaço-tempo, a taxa média de variação corresponde àquilo que correntemente se designa por velocidade média.

A velocidade média é dada por:

Por outras palavras, a velocidade média é a taxa média de variação quando a função é uma relação entre o espaço percorrido por um móvel e o tempo de percurso.

Velocidade instantânea - a velocidade instantânea ou simplesmente velocidade, v, do objecto para t = t0 é dada por:

Derivada de uma função num ponto: Seja y= f(x), definida no intervalo ]a, b[ , e seja x0 a abcissa de um ponto desse intervalo.
Chama-se derivada da função f no ponto de abcissa x0 e representa-se por f’(x0), ao limite, quando existe:

Função derivada: Chama-se função derivada, ou apenas derivada da função f e representa-se por f’ , Df á função que tem por domínio o conjunto dos pontos onde f admite derivada e que faz corresponder a cada um desses pontos o valor da respectiva derivada de f.

Sendo A o conjunto dos pontos onde f é derivável tem-se:

Exercicio - Taxa de Variação

A campanha publicitária

Durante uma campanha publicitária para a venda de uma certa marca de telemóveis, o número de unidades vendidas foi modelado por:


N(t) é em milhares de unidades e t em meses




2.1 - Determine a taxa média de variação do número de unidades vendidas nos primeiros dois meses de campanha e interprete o resultado no contexto de situação apresentada.

2.2 - justifique que:
A taxa média de variação pode ser positiva num intervalo e a função não ser crescente nesse intervalo.




Resolução:

2.1 -
Nos dois primeiros meses de campanha, o número de telemóveis vendidos aumentou a uma média de 2000 unidades por mês.



2.2 - Por exemplo:
A taxa média de variação é positiva.

Exercício - Taxa de Variação

Avalia - se que daqui a t anos. a circulação de um jornal local será dada pela função C(t) = 100t ao quadrado + 400t +5000 exemplares

1.1 - Deduza a expressão da taxa de variação da circulação do jornal daqui a t anos.

1.2 - Qual será a taxa de variação da circulação daqui a 5 anos?

1.3 - Qual a percentagem de variação da circulação do jornal daqui a 5 anos?




Resolução:

C(t) = 100t² + 400t +5000


1.1 - Para obter a expressão da taxa de variação da circulação em função do tempo em anos, usamos derivação implícita (Deriva-se os dois lados em função do tempo):

dC/dt = 2.100t + 400

Ou seja, a taxa de variação (Delta) é igual a:

dC/dt = 200t + 400



1.2 - Substituindo na equação encontrada no item a, temos:

dC/dt = 200t + 400
dC/dt = 200.5 + 400
dC/dt = 1000 + 400
dC/dt = 1400



1.3 - Percentagem da variação da circulação em relação a hoje:

dC/dt = 200t + 400

Hoje: dC/dt = 200.0 + 400 = 400
Daqui a 5 anos: 200.5 + 400 = 1400



Percentagem:

1400/400 = 3,5 = 350% (Aumento de 350%)

Exercicio - Taxa de Variação

Numa mercearia, uma maça foi lançada ao ar, de baixo para cima. A altura da maça de baixo para cima é dado por:

Onde t designa o tempo, em segundos, e h a altura, em metros.

1.1 - Calcule a taxa média de variação nos dois primeiros segundos após o lançamento.

1.2 - Calcule a taxa média de variação no intervalo [t, t + h], com h a tender para zero.

1.3 - Calcule a velocidade da maça no instante t = 2.

1.4 - Escreva uma equação da recta tangente ao gráfico de h no ponto de abcissa 1.

Resolução:

1.1 - Atendendo à expressão que permite calcular a taxa média de variação num intervalo [a,b], temos:

1.2 -

Como h tende para zero, temos:

1.3 - Pela definição de derivada, podemos concluir que h´ (t) = 8 – 2t.

Como a velocidade no instante t=2 corresponde á derivada de h no ponto de abcissa 2, temos então que:

A velocidade da maça no instante t=2 é de 4 m/

1.4 - Para escrever uma equação da recta tangente é necessário conhecer as coordenadas do ponto de tangencia, assim como o declive da recta.
O ponto de tangente tem abcissa igual a 1, logo, a coordenada é h (1)

Assim, o ponto de tangente tem de coordenadas (1,9)

Experiência - A Resistência do Esparguete

Material:

• Fio de pesca;



• Pequenos pesos todos iguais (moedas, ...);



• Vários paus de esparguete;



• Uma caixa leve (um saco plástico), para colocar dentro os pesos.

Experiência:

Coloque um pau de esparguete numa mesa, perpendicular ao bordo, com uma parte fora da mesa, tal como está na figura.

Prenda a caixa com o fio de pesca de forma a poder suspendê-la do pau de esparguete (coloque com fita-cola para o fio não deslizar do esparguete).
Meça o comprimento do esparguete que ficou para fora do bordo da mesa.
Coloque na caixa (e conte) os pesos, um a um, até o esparguete partir.
Registe o comprimento do esparguete e o número de pesos necessários para ele partir.
Repita a experiência várias vezes alterando o comprimento do esparguete.

1. Registe, os dados recolhidos, numa tabela:

2. Introduza os dados na calculadora e faça um gráfico que relacione o comprimento do esparguete com o número de pesos necessários para o partir.

3. Encontre uma função que descreva esta situação.

Sugestão 1: Multiplique as duas listas dos dados e analise os resultados.
Sugestão 2: Utilize uma das funções de regressão da calculadora.